- #DIGIT TO FRACTION CONVERTER HOW TO#
- #DIGIT TO FRACTION CONVERTER FREE#
If the "true" decimal value is actually repeating, how do I convert it to a fraction?.
If I see a decimal output that appears to terminate, how can I know if it is really just a truncated form of a repeating decimal with a long block of repeating digits?. So the real question ought to have three parts to it: But that is misleading you: That truncation cannot be converted into the form $572/1521$, because it isn't equal to $572/1521$. If you round this to fit on a calculator display, the result will look like $0.3760683761$. As Eric pointed out in his answer, $572/1521$ is actually equal to $0.376068~376068~376068 \dots$, with a repeating block of six digits. You confirm, by entering this into your calculator, that the results are equal, and want to know how you could have found the fraction yourself.īut here's the thing: those results are not equal. But the correct solution, according to the textbook, is $572/1521$. The calculator tells you the answer is $0.3760683761$. Using a graphing calculator or some other form of computer algebra system, you graph the polynomial and then use the technology's built-in numerical tools to find the location of the zero. You are trying to solve some kind of problem maybe it's "find the zeroes of such-and-such polynomial". Here is a (completely hypothetical, made-up) scenario that I suspect is not too far off the mark from what is going on here. The difficulty with this question - and it is one that has come up in the comments to several answers, but has not yet been explicitly addressed by any of the answers - is that it appears that the number you are actually interested in is not the number you think you are interested in. If you have a non-terminating non-repeating decimal then you cannot write it as a fraction. Note that I used $10^6=1000000$ in the solution as the repeating part of the decimal is six digits long. In the case of a repeating decimal, you can generalize the technique that I used above. Now if we have $\frac ab$ on the left and $\frac cd$ on the right, we should check $\frac$). They are not very good approximations though! First write $$\frac01 < 0.3760683761 < \frac11$$ so right away we have a pair of fractions that approximate 0.3760683761. Otherwise return from Converting Decimal to Fraction to Rules of Fractions.Here's a different way to proceed, using as little as possible of the theory of continued fractions. #DIGIT TO FRACTION CONVERTER FREE#
Use one of our free online math calculators to do it for you!. #DIGIT TO FRACTION CONVERTER HOW TO#
Learn how to convert percent to a fraction.Ĭonvert fractions to decimal: fraction to decimal chart.Ĭonvert between improper fractions and mixed numbers. Grade A offers plenty of other resources for converting between forms. If you are having trouble with step 3, let Grade A help you reduce fractions. Because both numbers cannot be reduced further, this is the final answer! When you divide them by 5 your fraction now becomes 3/20.
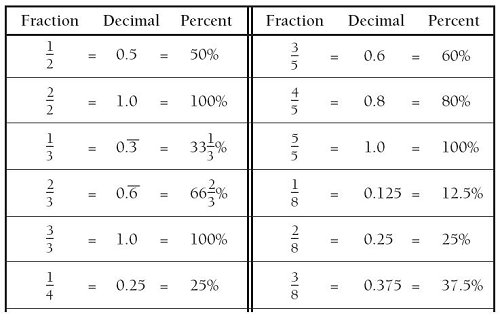
In this example, the top has two digits and the bottom has three. Another way to think about this is that the bottom should always have one more digit than the top. Step 2: the bottom of the fraction becomes 100 because 15 has two digits, so you need to put two 0's. Step 1: take all the numbers after the decimal point, 15, and place them on the top of the fraction - this is the numerator. In this example we are going to convert the decimal 0.15 into a fraction.ĭescription of each of the three steps above: Don't use this unless you understand the process above first - but once you do, it will be a real time save for you!Įxample of Decimal to Fraction Conversion Once you know the process for decimal to fraction conversion, Grade A has a nice shortcut for you: a free online decimal to fraction calculator. However many digits you have in the top, thats how many zeros you should have in the bottom!
In the bottom of the fraction put a multiple of 10 (10, 100, 1000, etc.). Take the numbers after the decimal point and put them in the top of the fraction. When you are converting decimal to fraction, remember these three easy steps:
0 kommentar(er)
